$ \newcommand\heartcard{\boxed{\color{red}{♥\,}}} \newcommand\clubcard{\boxed{♣\,}} \newcommand\commitedcard{\boxed{?\,}} \newcommand\heartclub{\heartcard\clubcard} \newcommand\clubheart{\clubcard\heartcard} \newcommand\twocommitedcards{\commitedcard\commitedcard} \newcommand\threecommitedcards{\commitedcard\commitedcard\commitedcard} $ 秘密計算といえば、通常コンピュータを用いて行うものですが、トランプ(のようなもの)を用いることで、コンピュータを用いずに秘密計算を行うという研究があります。
秘密の足し算
今回の目標は、まず A と B という人物がそれぞれ数字$x_A$と$x_B$を持っているとして、その数字を互いに知られることなく$x_A + x_B$を計算することです。
利用するカード
ここでは
- $\heartcard$
- $\clubcard$
という二種類のカードを考えます。ただしこのカードは両方とも裏面が$\commitedcard$となっており、裏になったカードを区別することはできないものとします。
エンコーディング
二種類のカードを使って次のようにブール値をエンコードします。
- $\clubheart = 0$
- $\heartclub = 1$
半加算器
ブール値の計算を行うために半加算器を使います。これは二つのブール値を受け取り次のような計算をします。
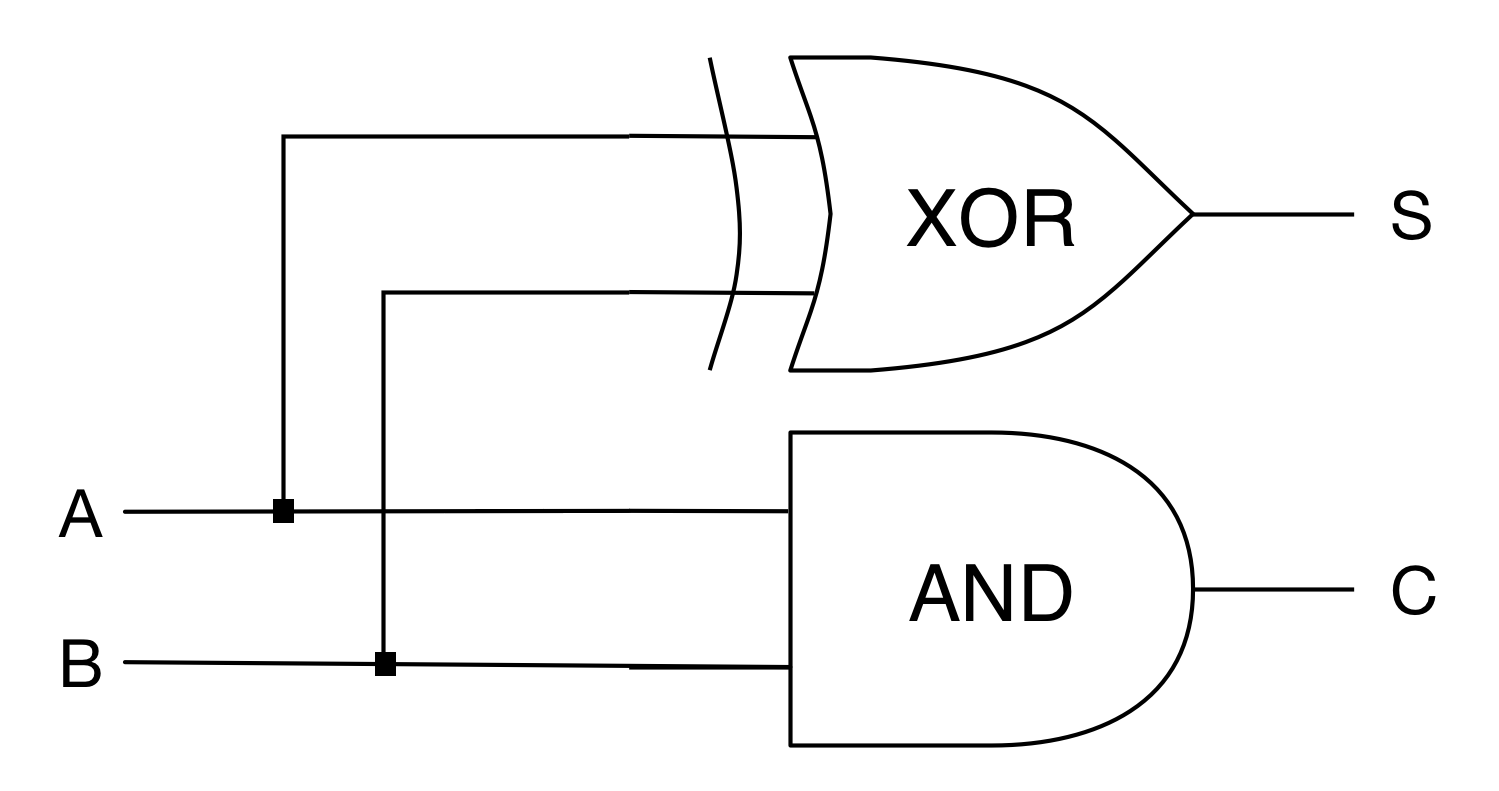
$S$が$A$と$B$を計算した後のビットに対応し、$C$はキャリーを示します。真理値表は次のようになります。
| A | B | S | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
この半加算器を作るためには次の三つの操作を秘密に行う必要があります。
- AND演算
- XOR演算
- コピー
ここで、コンピュータ上のコピーは簡単な操作ですが、裏向きになった二枚カードと同じ状態の二枚のカードを作るというのは工夫が必要です。
全加算器
二進数の足し算は半加算器を使って次のように表現できます。(図中の四角は半加算器です) $A$と$B$は足し算するビットで、$X$はキャリーです。
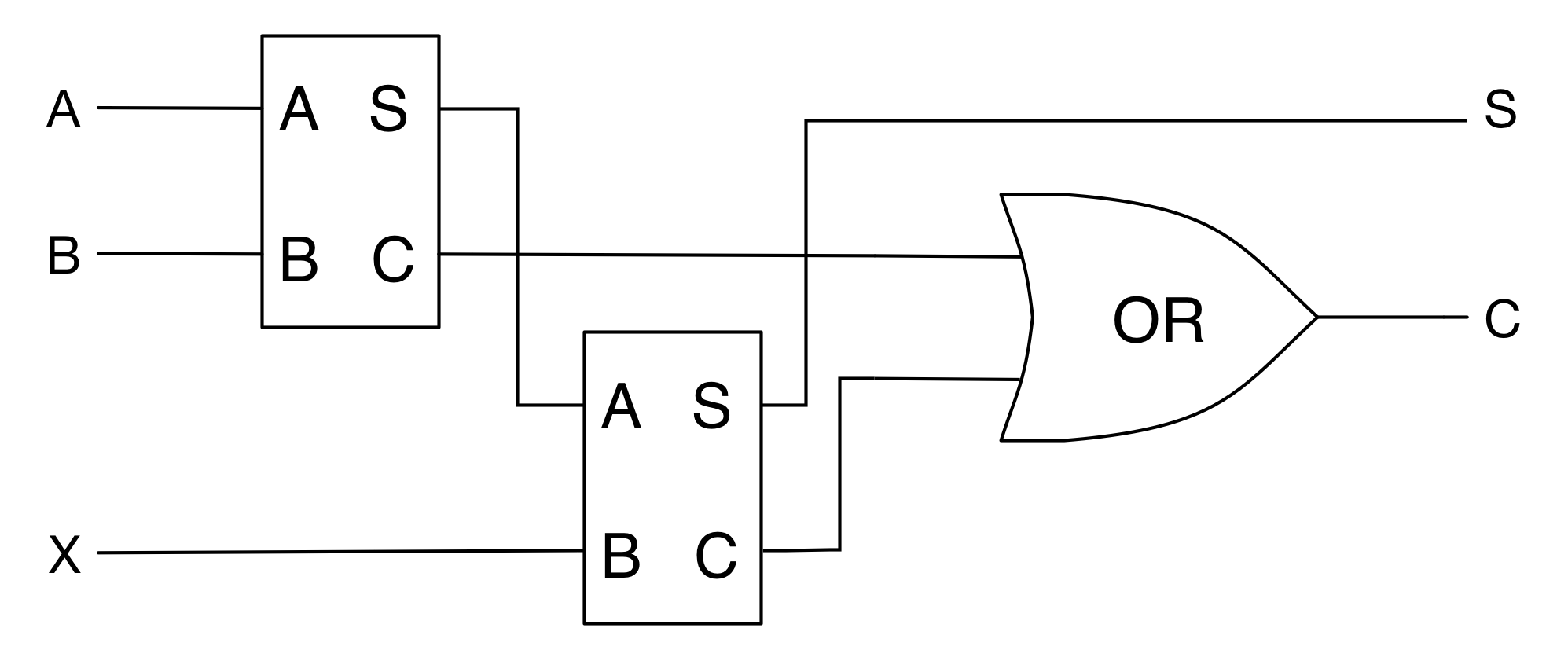
ここでOR演算が新たに必要になります。
ブール演算
先ほど挙げた、AND、XOR、NOTそしてコピーを秘密にカードで表現する方法を紹介します。ここで秘密にとは、カードを表にすることなく、演算を行うということです。
NOT演算
裏向きになった二枚のカードの、右と左のカードを入れ替えるだけです。
\[ \underset{1}{\commitedcard}\,\underset{2}{\commitedcard} \rightarrow \underset{2}{\commitedcard}\,\underset{1}{\commitedcard} \]ランダム二等分カット(random bisection cut)
ANDやXOR演算を実装するにあたって、次の操作を定義する必要があります。 カードを半分に分けて、50%の確率で二つの位置を入れ替える操作です。
\[ \newcommand\rbc[2]{\left[#1 \mid\mid #2\right]} \rbc{\underbrace{\threecommitedcards}_{A}}{\underbrace{\threecommitedcards}_{B}} \\ \Downarrow\\ \underbrace{\threecommitedcards}_{A}\,\underbrace{\threecommitedcards}_{B} \;\text{or}\;\underbrace{\threecommitedcards}_{B}\,\underbrace{\threecommitedcards}_{A} \]AND演算
入力として二枚ずつのカード(計四枚)を受け取り、それとは別にカードを二枚、合計で六枚のカードを用いて次のようにANDを計算します。
\[ \underbrace{\twocommitedcards}_{A}\, \underbrace{\twocommitedcards}_{B} \, \clubheart \Rightarrow \underbrace{\twocommitedcards}_{A \wedge B} \]次のような流れになります。
- 追加のカードを裏にする
- カードの順序を入れ替える($2 \rightarrow 4, 3 \rightarrow 2, 4 \rightarrow 3$)
- ランダム二等分カットを実行する
- カードの順序を入れ替える($2 \rightarrow 3, 3 \rightarrow 4, 4 \rightarrow 2$)
- 左から二枚を表にして、$\clubheart$なら右から二枚が$A \wedge B$の結果となる。$\heartclub$なら真ん中の二枚が$A \wedge B$の結果となる。
OR演算
AND演算と同じような方法で次のようにできます。
\[ \underbrace{\twocommitedcards}_{A}\, \underbrace{\twocommitedcards}_{B} \, \heartclub \\ \Downarrow \\ \underbrace{\twocommitedcards}_{A}\, \underbrace{\twocommitedcards}_{B} \, \underbrace{\twocommitedcards}_{1} \\ \Downarrow \\ \underset{1}{\commitedcard}\,\underset{2}{\commitedcard}\, \underset{3}{\commitedcard}\,\underset{4}{\commitedcard}\, \underset{5}{\commitedcard}\,\underset{6}{\commitedcard} \rightarrow \underset{1}{\commitedcard}\,\underset{3}{\commitedcard}\, \underset{4}{\commitedcard}\,\underset{2}{\commitedcard}\, \underset{5}{\commitedcard}\,\underset{6}{\commitedcard} \\ \Downarrow \\ \rbc{\threecommitedcards}{\threecommitedcards} \\ \Downarrow \\ \underset{1}{\commitedcard}\,\underset{2}{\commitedcard}\, \underset{3}{\commitedcard}\,\underset{4}{\commitedcard}\, \underset{5}{\commitedcard}\,\underset{6}{\commitedcard} \rightarrow \underset{1}{\commitedcard}\,\underset{4}{\commitedcard}\, \underset{2}{\commitedcard}\,\underset{3}{\commitedcard}\, \underset{5}{\commitedcard}\,\underset{6}{\commitedcard} \\ \Downarrow \\ \clubheart\, \underbrace{\twocommitedcards}_{A \vee B} \, \twocommitedcards \; \text{or} \; \heartclub\, \twocommitedcards \, \underbrace{\twocommitedcards}_{A \vee B} \]XOR演算
二枚ずつの入力(計四枚)のみで次のように行います。
- カードの順序を入れ替える($2 \rightarrow 3, 3 \rightarrow 2$)
- ランダム二等分カットを実行する
- カードの順序を入れ替える($2 \rightarrow 3, 3 \rightarrow 2$)
- 左から二枚を表にして、$\clubheart$なら右から二枚が$A \oplus B$の結果となる。$\heartclub$なら$\overline{A \oplus B}$の結果となる。
コピー
ある入力(二枚)をコピーするために、四枚のカードを追加し次のようにします。
- $\clubheart(= 0)$をコピーしたいカードの右に二組追加する
- カードの順序を入れ替える($2 \rightarrow 4, 3 \rightarrow 2, 4 \rightarrow 5, 5 \rightarrow 3$)
- ランダム二等分カットを実行する
- カードの順序を入れ替える($2 \rightarrow 3, 3 \rightarrow 5, 4 \rightarrow 2, 5 \rightarrow 4$)
- 左から二枚を表にして、$\clubheart$なら残りの四枚に入力がコピーされる。$\heartclub$なら入力にNOT演算をしたものがコピーされる。
まとめ
これらのブール値の演算を使って半加算器を実装し、半加算器で全加算器を実装すればよいということになります。 もし力が残っていれば、例を出してやってみたいです。
参考文献
大変おもしろいスライドです。
コメント
コメントを投稿