リストへ何度もランダムにアクセスする際の効率的な方法

この記事にあるコードは下記のGistにまとめてあります。 https://gist.github.com/yoshimuraYuu/96ca584da1d04efb248b

例えば数字$0, 1, \dots, 25$からアルファベット$a, b, \dots, z$へ変換するために次のようなリストを定義したとします。

let alphabet = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h'; 'i'; 'j'; 'k'; 'l'; 'm'; 'n'; 'o'; 'p'; 'q'; 'r'; 's'; 't'; 'u'; 'v'; 'w'; 'x'; 'y'; 'z']

ここでは例として、1から25までの数字で構成されたリストを受け取って、それを上記のリストを用いて文字のリストへ変換する関数を作るとします。

直感的な実装

まず、リストを先頭から調べていって$n$番目の要素を返す関数nthを定義します 1。

let rec nth l = function
    0   ->  List.hd l
|   i   ->  nth (List.tl l) (i - 1)

このnthを使って、入力されたリストに対応するリストalphabetの要素を返す関数を次のように定義します。

let rec trans1 = function
    []      -> []
|   x::xs   -> nth alphabet x :: trans1 xs

まずnthは$n$回再帰するので、計算量$O(n)$の関数ということになります。その関数をリストの長さ分呼び出しているtrans1の計算量は、リストの長さを$n$、要素の平均を$m$とすると$O(n \times m)$という計算量になります。

次のようなテストする関数で試してみます。この関数は引数lとnを取り、trans1 lを$n$回繰り返す関数です。

let rec test1 l = function
    0   -> ();
|   i   -> 
        let _ = trans1 l in
        test1 (i - 1)

次の例をtimeコマンドでどれくらいかかるのか測定してみます。

test1 [1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1] 1000000
$ time ocaml trans.ml
ocaml trans.ml  2.09s user 0.01s system 99% cpu 2.101 total

一方で、この例は大変なことになります。

test1 [25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25] 1000000
$ time ocaml trans.ml
ocaml trans.ml  15.36s user 0.02s system 99% cpu 15.503 total

この差を埋めるのが当面の目標です。

効率的な実装

リストを「インデックスでソートされた二分木」へ変換します。 まずは木を次のように定義します。NはノードでLはリーフを表します。

type 'a tree =
    L of 'a
|   N of int * 'a tree * 'a tree

二分探索のように、要素を半分半分にしていく関数を定義します。

let join = function
    ((L _) as t1), ((L _) as t2)                  -> N(2, t1, t2)
|   ((L _) as t1), ((N(n, _, _)) as t2) |
    ((N(n, _, _)) as t1), ((L _) as t2)           -> N(n + 1, t1, t2)
|   ((N(n1, _, _)) as t1), ((N (n2, _, _)) as t2) -> N(n1 + n2, t1, t2)

let rec inner = function
    []          -> []
|   x::[]       -> [x]
|   x::(y::xs)  -> (join (x, y)) :: inner xs

let rec build_tree = function
    x::[]       -> x
|   xs          -> build_tree (inner xs)

複雑ですが、イメージはこんな感じです。

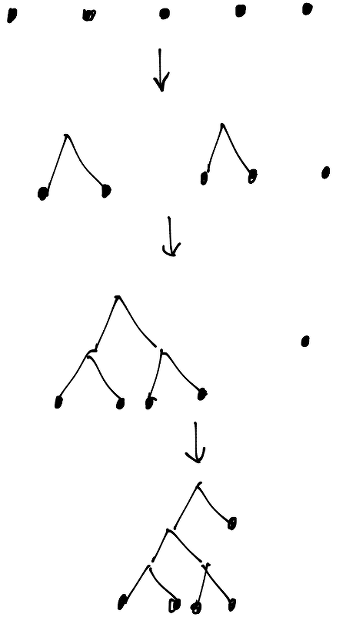
buil_tree_reduce.png

アルファベットのリストを一旦二分木へ変換すると、次のようになります。

# build_tree (List.map (fun x -> L x) alphabet);;
- : char tree =
N (26,
 N (16,
  N (8, N (4, N (2, L 'a', L 'b'), N (2, L 'c', L 'd')),
   N (4, N (2, L 'e', L 'f'), N (2, L 'g', L 'h'))),
  N (8, N (4, N (2, L 'i', L 'j'), N (2, L 'k', L 'l')),
   N (4, N (2, L 'm', L 'n'), N (2, L 'o', L 'p')))),
 N (10,
  N (8, N (4, N (2, L 'q', L 'r'), N (2, L 's', L 't')),
   N (4, N (2, L 'u', L 'v'), N (2, L 'w', L 'x'))),
  N (2, L 'y', L 'z')))

この二分木から$n$番目の文字を取り出す関数を次のように定義します。

let rec extract_tree = function
    0, N(_, (L e), r)     -> e
|   1, N(2, (L _), (L r)) -> r
|   n, N(_, (L _), r)     -> extract_tree (n - 1, r)
|   n, N(n1, l, (L e)) when n + 1 == n1 -> e
|   n, N(c, (N(cl, _, _) as l), r) ->
        if n < cl then
            extract_tree (n, l)
        else
            extract_tree (n - cl, r)
|   _   -> failwith "error"

まず、extract_treeに0と左がリーフの木が渡された場合、左側の木の要素を返します。

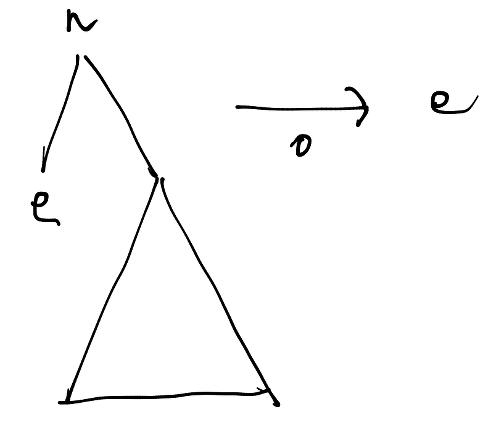
extract1_reduce.png

次に左がリーフで右もリーフの大きさ2の木に対して、1が入力された場合は次のようになります。

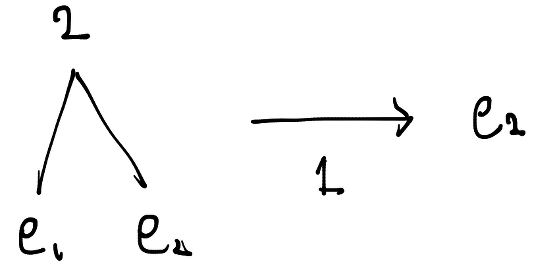
extract2_reduce.png

左がリーフで右がノードの場合、右のノードを再帰的に調べていきます。

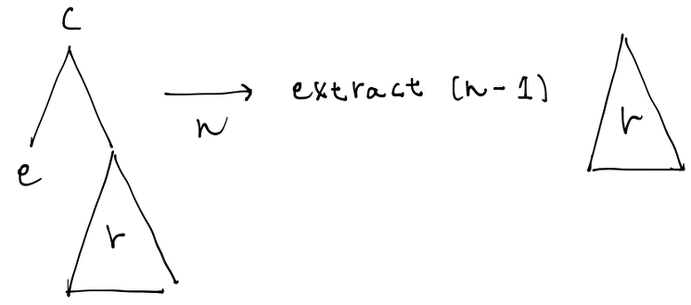
extract3_reduce.png

左がノードで右がリーフの場合、次のような条件で右のリーフの要素を返します。

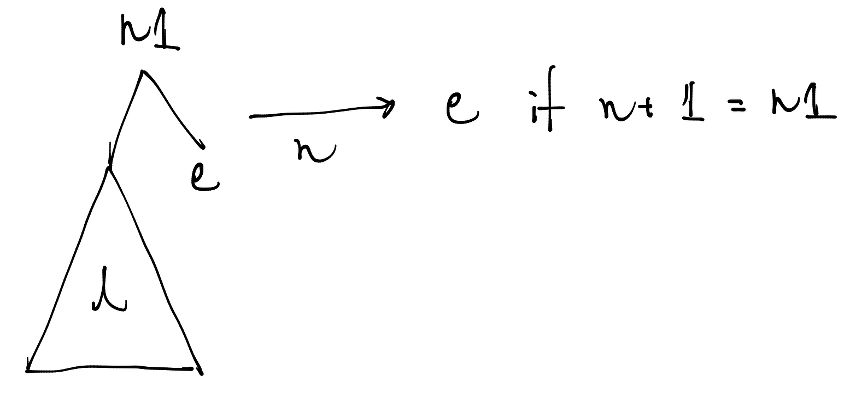
extract4_reduce.png

右と左が両方ノードである場合は入力nに応じて次の二つに分岐します。

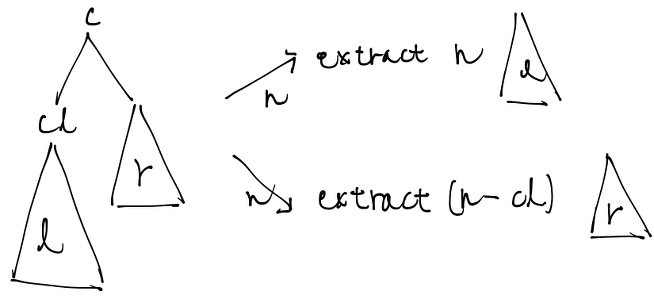
extract5_reduce.png

しっかり取り出せるのかを、次のコードで検証します。

let alphabet_tree = build_tree (List.map (fun x -> L x) alphabet)
let check_extract_tree () = 
    let rec loop i =
        if i > 25 then []
        else extract_tree (i, alphabet_tree) :: loop (i + 1)
    in
    loop 0
# check_extract_tree ();;
- : char list =
['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h'; 'i'; 'j'; 'k'; 'l'; 'm'; 'n'; 'o';
 'p'; 'q'; 'r'; 's'; 't'; 'u'; 'v'; 'w'; 'x'; 'y'; 'z']

そして、数字のリストからアルファベットのリストへ変換する効率的な関数を定義します。

let rec trans2 l =
    match l with
        []      -> []
    |   x::xs   -> extract_tree (x, alphabet_tree) :: trans2 xs

テスト用のコードを用意します。

let rec test2 l = function
    0   -> ();
|   i   -> 
        let _ = trans2 l in
        test2 l (i - 1);;

それではテストです。

test2 [1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1] 1000000
$ time ocaml trans.ml
ocaml trans.ml  9.55s user 0.01s system 99% cpu 9.557 total

どれくらいの差があるでしょうか。

test2 [25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25; 25] 1000000
$ time ocaml trans.ml
ocaml trans.ml  5.64s user 0.01s system 99% cpu 5.652 total

test1に比べて差が少ないようです。

結論

リストから二分木へ変換する計算量は、リストの長さを$n$として$O(\log_2(n))$です。この二分木から要素を取り出す計算量は$O(\log_2(n))$なので、trans2 lはlの長さを$m$とすると、$O\left((m + 1) \log_2(n)\right)$ということになります。 直感的な実装の計算量が$O(n \times m)$なので、こちらの実装の方が効率的であると言えそうです。

参考文献

  1. OCamlにはList.nthという機能が同じ関数がありますが、ここではnthの動作を分かりやすくするために、あえて再実装しました。↩

コメント

コメントを投稿